Mga kategorya: Itinatampok na Mga Artikulo » Mga bagyong elektrisista
Bilang ng mga tanawin: 57937
Mga puna sa artikulo: 4
Boolean algebra. Bahagi 3. Mga scheme ng pakikipag-ugnay
 Inilalarawan ng artikulo ang mga pangunahing prinsipyo ng pagdidisenyo ng mga circuit ng relay alinsunod sa isang naibigay na algorithm ng kanilang operasyon.
Inilalarawan ng artikulo ang mga pangunahing prinsipyo ng pagdidisenyo ng mga circuit ng relay alinsunod sa isang naibigay na algorithm ng kanilang operasyon.
Sa dalawa nakaraang mga artikulo ay sinabi tungkol sa mga pangunahing kaalaman Boolean algebra at relay algebra. Sa batayan na ito, ang mga istrukturang pormula ay binuo, at ang mga tipikal na contact circuit ay binuo sa kanila.
Ang pagguhit ng isang istruktura na formula ayon sa isang yari na pamamaraan ay isang simpleng bagay. Mas mahirap ipakita ang electrical circuit ng hinaharap na makina ayon sa yari na pormula ng istruktura. Kailangan ng ilang pagsasanay!
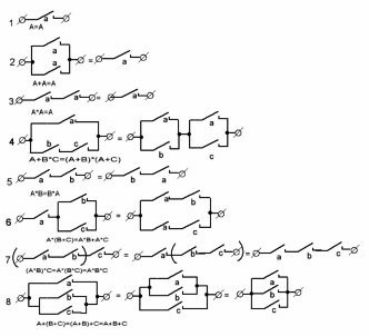
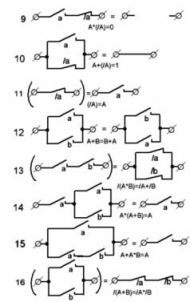
Ipinapakita ng Figure 1 ang pinaka-karaniwang mga pagpipilian. makipag-ugnay sa mga circuit at ang kanilang mga katumbas. Makakatulong sila sa paghahanda ng mga de-koryenteng circuit ng mga makina, pati na rin pag-aralan ang mga yari na istraktura, halimbawa, sa proseso ng pag-aayos ng mga ito.
Paano mo magagamit ang mga pagpipilian para sa mga circuit ng contact na tinalakay sa itaas?
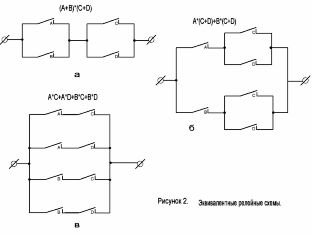
Isaalang-alang ang circuit na ipinakita sa Figure 2, a. Ang kaukulang pormula ng istruktura ay may form: (A + B) * (C + D).
Gamit ang batas ng pamamahagi ng Boolean algebra, binubuksan namin ang mga bracket sa expression na ito at nakuha ang: A * (C + D) + B * (C + D), na tumutugma sa scheme na ipinakita sa Figure 2, b. Karagdagan, dahil sa pagdami, makakakuha tayo ng pormula A * C + A * D + B * C + B * D, na naaayon sa Larawan 2, c.
Ang lahat ng tatlong mga scheme ay katumbas, iyon ay, lumiliko silang sarado sa ilalim ng parehong mga kondisyon. Gayunpaman, naiiba ang mga ito sa pagiging kumplikado.
Larawan 1. Karaniwang mga circuit ng contact
Ang una sa mga circuit, ang pinakasimpleng, nangangailangan ito ng apat na relay, ang bawat isa ay dapat magkaroon ng isang normal na bukas na contact. (Upang gawing simple ang mga guhit, hindi ipinapakita ang mga relay coil).
Ang Scheme "b" ay nangangailangan ng isang relay sa dalawang grupo ng contact. Sa totoo lang, ang pangunahing gawain ng algebra ng mga contact circuit ay upang mahanap ang lahat ng mga katumbas na circuit upang maaari mong piliin ang pinakasimpleng isa mula sa kanila.
Larawan 2. Katumbas na mga circuit ng contact.
Upang pagsamahin ang materyal na sakop, subukang lutasin ang mga sumusunod na problema sa iyong sarili.
1. Iguhit ang diagram ng circuit ng isang automaton na may istrukturang pormula A * B * C * D + A * B * E + A * D.
2. Patunayan na ang mga circuit na ipinakita sa Figure 3, a at b, ay katumbas.
3. Pasimplehin ang circuit na ipinakita sa Larawan 3, c.
4. Anong pormula ng istruktura ang nagpapatupad ng scheme sa Larawan 3, d?
Matapos ang napag-aralan na natin, posible na magsimula upang malutas ang mga problema na itinakda sa pinakadulo simula ng unang artikulo. Naaalala namin ang mga ito sa madaling sabi.
Ang unang gawain ay upang i-on at i-off ang ilaw na bombilya sa silid na may tatlong switch na matatagpuan sa iba't ibang mga lugar: sa pinto, sa mesa, sa kama.
Ang pangalawang gawain ay ang pagboto ng mga hukom sa palakasan: mula sa apat na hukom na "PARA" ay dapat bumoto ng hindi bababa sa dalawa, sa kondisyon na bumoto ang "PARA" sa chairman ng komisyon.
Ang pangatlong gawain ay para lamang sa mga layuning pang-edukasyon. Iminungkahi nito ang pareho tulad ng una, para lamang sa anim na switch, na tila mayroong anim na pader sa silid. Ang mga katulad na circuit ay binuo lamang gamit ang algebra ng mga relay circuit.
Sa pangkalahatan, kung nais naming bumuo ng isang scheme na may ilang naibigay na lohikal na mga katangian, pagkatapos ay maaari naming lapitan ang problemang ito sa dalawang magkakaibang paraan. Ayon sa kombensyon, ang mga landas na ito ay maaaring tawaging "intuitive" at "algebraic".
Ang ilang mga gawain ay mas mahusay na malulutas sa unang paraan, habang ang iba sa pangalawa. Ang intuitive na pamamaraan ay lumiliko na maging mas maginhawa kapag ang operasyon ng circuit ay kinokontrol ng maraming mga switch, ngunit mayroong ilang simetrya sa magkakasamang pagsasaayos ng mga relay na ito. Makikita natin na narito ang isang madaling maunawaan na diskarte ay humahantong sa layunin nang mas mabilis, habang ginagamit ang apparatus ng relay algebra sa kaso ng maraming mga variable ay maaaring maging masalimuot. Ito ay kapaki-pakinabang upang makilala ang parehong mga posibleng pamamaraan sa paglutas ng problemang ito.
Magsimula tayo sa isang madaling gamitin na diskarte. Ipagpalagay na kailangan naming bumuo ng isang circuit na sarado kapag gumana ang lahat ng mga kontrol ng relay n.
Ang solusyon sa problemang ito ay hindi nangangailangan ng mahabang konsultasyon: malinaw na ang kondisyon ay matutupad kung magkakaugnay na sunud-sunod na n normal na bukas na mga contact ng relay.
Katulad nito, malinaw na ang pagbuo ng isang circuit na nagsasara kung hindi bababa sa isa sa mga n relay ay nakakulong, sapat na upang kumonekta n normal na bukas ang mga contact ng relay na magkatulad.
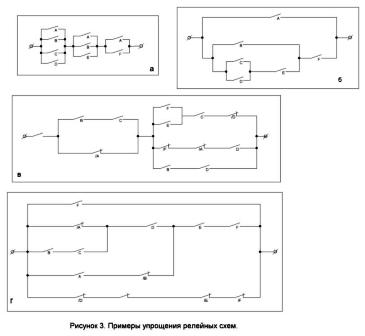
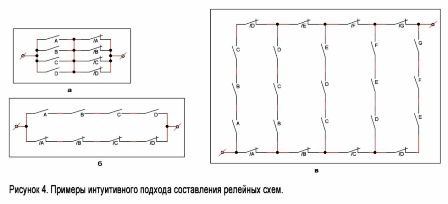
Madaling isipin ang isang circuit na nagsasara kapag ang ilan, ngunit hindi lahat, ang mga relay ay na-trigger. Ang nasabing circuit ay ipinapakita sa Figure 4, a. Sa kanan ay isang diagram na nagpapatakbo sa prinsipyo ng "lahat o wala." Ito ay sarado lamang kapag ang lahat ng mga relays biyahe o ang mga relay ay na-disconnect (Larawan 4, 6).
Isaalang-alang ngayon ang isang mas kumplikadong halimbawa. Ipagpalagay na mayroong mga contact na matatagpuan sa isang tiyak na pagkakasunod-sunod: A, B, C, D, E, F ... Nagtatayo kami ng isang circuit na nagsasara kapag ang anumang mga contact na serye ng k ay nakasara, at sila lamang. Ang ganitong pamamaraan para sa mga halaga n = 7 at k = 3 ay ipinapakita sa Figure 4, c. Ang pamamaraan para sa pagtatayo ng naturang mga scheme para sa anumang iba pang mga halaga ng n at k ay malinaw mula sa figure na ito.
Nagpapatuloy kami sa pagtatayo ng mga circuit ayon sa ibinigay na mga kondisyon ng kanilang trabaho gamit ang relay algebra.
Tulad ng dati, ang mga kondisyon ng operating ng circuit ay palaging palaging unang itinakda nang pasalita. Ang taga-disenyo, una sa lahat, ay dapat na ilagay sa mga salita ang nais niya. Kung wala siyang kalinawan, walang makakatulong sa algebra. Dapat mong palaging magsimula sa isang malinaw na pahayag ng mga kinakailangan na itinakda bago ang bagong pamamaraan. Tulad ng sa anumang negosyo, ang gawaing ito ay marahil ang pinakamahirap. Kung ang mga kondisyon ay sapat na simple, pagkatapos ay maaari naming agad na magsulat ng isang expression ng isang pormula sa istruktura na nasiyahan sa mga kinakailangang ito.
Halimbawa 1 Ipagpalagay na kailangan nating magtayo ng isang circuit na naglalaman ng 4 na pin ng A, B, C at D upang ang circuit ay nakabukas kapag ang contact A ay sarado, at isa sa iba pang tatlong mga contact. Sa simpleng kaso na ito, ang pagpapatakbo ng circuit sa pagsulat ng pandiwang ito ay magiging ganito: "Ang circuit ay dapat magsagawa ng kasalukuyang kung ang mga contact A at B ay sarado, o mga contact A at C o mga contact A at D. Sumasang-ayon na ngayon ay napaka-simple upang gumuhit ng isang istruktura na pormula. Mukhang ganito:
A * B + A * C + A * D = 1 o A * (B + C + D) = 1.
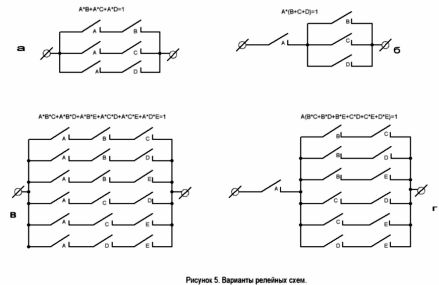
Ang circuit ay may dalawang pagpipilian. Ang mga ito ay ipinapakita sa Figure 5. Ang pangalawang pagpipilian ay hindi nangangailangan ng isang relay na may tatlong normal na bukas na contact.
Halimbawa 2 Ang unang artikulo ay task number 2 sa pagboto ng mga hukom sa sports. Basahin ang kalagayan nito nang mas malapit, ito ay katulad ng halimbawa na napagmasdan. Ang isang mas malinaw na rekord ng pandiwa sa mga kinakailangan ay magiging ganito: "Kinakailangan upang gumuhit ng isang circuit na naglalaman ng 5 mga contact A, B, C, D, E, upang magsagawa ng kasalukuyang at i-on ang display lamp kung sarado ang mga sumusunod na contact:
A at B at C, o A at B at D, o A at B at E, o A at C at D, o A at C at E, o A at D at E. Makipag-ugnay sa A ay ang pindutan ng chairman. Kung hindi ito pinindot, pagkatapos ang bawat isa sa 6 na mga lohikal na produkto ay magiging 0, i.e. Hindi naganap ang pagboto.
Ang pormula ng istruktura ay ang mga sumusunod:
(A * B * C) + (A * B * D) + (A * B * E) + (A * C * D) + (A * C * E) + (A * D * E) = 1,
o A * (B * C + B * D + B * E + C * D + C * E + D * E) = 1.
Ang parehong mga variant ng circuit ay ipinapakita sa Figure 5, c at d. Ito ang solusyon sa problema.
Ang pagkakaroon ng ilang mga kasanayan sa pagbabasa ng mga pormula ng istruktura, madaling isipin ang circuit ng automaton mismo at lahat ng mga kakayahan nito. Kapansin-pansin, ang algebra ng mga relay circuit ay nagbibigay ng maraming impormasyon kaysa sa mismong circuit mismo. Pinapayagan ka nitong makita kung ilan at kung aling mga relay ang kinakailangan. Sa tulong nito, madali mong mahahanap ang pinakasimpleng bersyon ng circuit machine.
Halimbawa 3 Ang pagkakaroon ng pagkakaroon ng ilang karanasan sa paghahanda ng mga istruktura na pormula, susubukan naming lutasin ang problema na nagsimula unang artikulo: kailangan mong magdisenyo ng isang switch na nagbibigay-daan sa iyo upang buksan ang ilaw kapag pumapasok sa pasukan at patayin pagkatapos mong umakyat sa nais na palapag, o, sa kabilang banda, i-on ito kapag umalis sa apartment at patayin ito pagkatapos mong bumaba. Ang parehong sitwasyon ay nangyayari sa isang mahabang koridor: sa isang dulo, ang bombilya ay dapat na naiilawan, at pagkatapos ng pagpunta sa kabilang dulo, napapatay. Sa madaling sabi, ang gawain ay kumulo sa pagkontrol sa isang ilaw na bombilya mula sa iba't ibang mga lugar na may dalawang switch.
Pinipili namin ang sumusunod na pamamaraan para sa paglutas ng problema: una, malinaw naming bumalangkas ang mga kondisyon ng operating ng mga switch, pagkatapos ay isusulat namin ang mga ito sa anyo ng isang pormula, at iguguhit namin ang isang electric circuit gamit ang mga ito.
Kaya, na ang bombilya ay sumunog (1), kinakailangan na ang isa sa dalawang kondisyon ay natupad:
1. I-on ang switch sa ibaba (A) at i-off sa tuktok (/ B). Ipasok ang beranda.
2. I-on ang switch sa itaas (B) at i-off ang ibaba (/ A) Iwan ang apartment.
Gamit ang tinatanggap na notasyon, ang pormula ng istruktura ay nakasulat tulad ng sumusunod:
A * (/ B) + (/ A) * B = 1
Ang diagram ng circuit ng switch ay ipinapakita sa Larawan 6. Sa kasalukuyan, ang mga naturang switch ay magagamit nang komersyo, ito ay mga switch ng feedthrough. Samakatuwid, ang pagsasaalang-alang ng mga scheme dito ay ibinigay para sa konsepto ng pangkalahatang mga prinsipyo ng kanilang gawain.
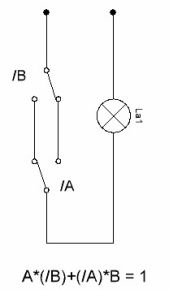
Larawan 6
Sa gawain Hindi. 1 sa simula ng unang artikulo, pinag-uusapan namin ang tungkol sa isang pamamaraan na nagpapahintulot sa iyo na i-on at i-off ang ilaw sa silid na may alinman sa tatlong switch. Nangangatuwiran sa parehong paraan tulad ng sa kaso ng dalawang switch, nakukuha namin ang pormula ng istruktura:
A * B * (/ C) + A * (/ B) + (/ A) * B * C = 1.
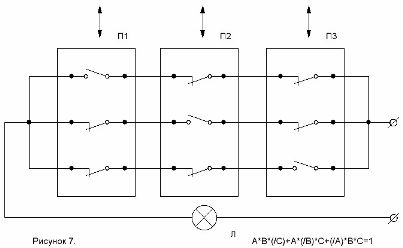
Ang pamamaraan na iginuhit ng formula na ito ay ipinapakita sa Figure 7.
Larawan 7
Sa simula ng unang artikulo, ang isang simpleng gawaing pang-edukasyon Blg. 2 ay iminungkahi: na parang mayroong anim na pader sa silid, at ang bawat isa ay may switch. Ang lohika ng circuit ay eksaktong kapareho ng para sa tatlong switch. Ipaalam sa amin ang mga ito sa pamamagitan ng mga titik A, B, C, D, E, F. Alalahanin na ang notasyon (/ A), (/ B) at iba pa, hindi ito isang sign sign, ngunit isang lohikal na negasyon. Mas madalas na ipinahiwatig ng mga salungguhit na character at, kahit na ang buong expression, sa itaas. Sa ilang mga scheme, ang underscore na ito ay simpleng pinalitan ng isang minus sign. Kaya, ang pormula ng istruktura para sa anim na switch ay:
(/ A) * B * C * D * E * F + A * (/ B) * C * D * E * F + A * B * (/ C) * D * E * F + A * B * C *
(/ D) * E * F + A * B * C * D * (/ E) * F + A * B * C * D * E * (/ F) = 1.
Inaanyayahan ang mga mambabasa na gumuhit ng isang kumpletong de-koryenteng circuit na nagpapatupad ng pormula ng istrukturang ito upang makakuha ng mga praktikal na kasanayan sa pagdidisenyo ng mga circuit. Isang maliit na pahiwatig: para sa circuit kakailanganin mo ng anim na relay, ang bawat isa ay mayroong isang normal na bukas na contact at limang normal na sarado. Ang nasabing kumplikadong relay, kung kinakailangan, ay maaaring tipunin mula sa ilang mga mas simple sa pamamagitan ng pagkonekta ng kanilang mga coils kahanay.
Natapos nito ang kwento ng Boolean algebra at ang algebra ng mga relay circuit.
Pagpapatuloy ng artikulo: Logic chips
Boris Aladyshkin
Tingnan din sa electro-tl.tomathouse.com
: