Boolean algebra. Bahagi 1. Kaunting kasaysayan

Sa paaralan, nag-aral kaming lahat ng algebra, ngunit hindi nila napag-usapan ang tungkol sa Boolean algebra. Ano ang pagkakaiba sa pagitan ng Boolean algebra at algebra ng paaralan, ang kasaysayan ng hitsura nito, mga problema at aplikasyon ay inilarawan sa artikulong ito.

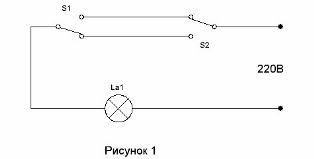
Ang circuit na nagbibigay-daan sa dalawang switch upang i-on ang ilaw sa pasilyo sa pasukan sa corridor at patayin ito kapag ang pagpasok sa silid ay kilala sa mahabang panahon (tingnan. Pagkontrol sa Pag-iilaw ng Koridor) Ipinapakita ito sa Figure 1.

Task number 1. Mas kumplikado. Lumikha ng isang diagram na nagbibigay-daan sa iyo upang i-on at i-off ang ilaw sa iyong silid na may alinman sa 3 magkakaibang switch. Ang mga switch ay matatagpuan sa pasukan sa silid, sa itaas ng kama at sa desk.

Gawain bilang 2.

Sa isang komite ng sports, tulad ng isang committee committee, nagtipon ang 5 hukom.

Ang bawat isa sa kanila ay dapat bumoto para sa iba't ibang mga pagpapasya. Ang pagpapasya ay pinagtibay ng isang mayorya ng mga boto, ngunit sa ilalim lamang ng karagdagang kundisyon na iboto ito ng chairman ng komite.

Ang mga hukom ay bumoto sa pamamagitan ng pagpindot sa pindutan na nagsasara sa switch na matatagpuan sa ilalim ng mesa kung saan sila nakaupo. Ang pagsasara ng switch, bumoto sila sa pabor, pag-disconnect ng cons. Gumuhit ng isang simpleng diagram na nagbibigay-daan sa iyo upang awtomatikong makita ang mga resulta ng pagboto. Sa pinakasimpleng kaso, sa tulong lamang ng isang ilaw na bombilya - naiilawan - ang desisyon ay ginawa, hindi tumindi - hindi.

Gawain bilang 3. Sa pagsasagawa, hindi ito malamang, ngunit bilang isang kumplikadong gawain sa pang-edukasyon ay lubos na angkop.

Sa isang malaking silid na heksagonal, ang isang switch ay naka-install sa bawat dingding. Gumawa ng isang circuit upang sa anumang oras maaari mong i-on o i-off ang ilaw sa silid sa pamamagitan ng pag-on ng isa (anumang) lumipat.

Matapos mong hindi matagumpay na umupo sa mga gawain nang tatlo hanggang apat na araw, itabi ang mga ito nang pansamantalang. At maging abala Boolean algebra. Ito ay ang Boolean algebra, o, tulad ng tinatawag din na, Boolean algebra, relay circuit algebra, tutulong sa iyo na malutas ang iyong mga problema.

Ano ang Boolean algebra?

Nakatutuwang sapat, sa kabila ng katotohanan na sa loob ng limang taon na sila ay nag-aaral ng algebra sa paaralan, maraming mga mag-aaral, at kalaunan ang mga matatanda, ay hindi masasagot ang tanong, ano ang algebra? Ang Algebra ay isang agham na nag-aaral ng mga hanay ng ilang mga elemento at ang mga aksyon sa kanila.

Sa isang kurso ng paaralan sa algebra, ang mga naturang elemento ay mga numero. Ang mga numero ay maaaring ipahiwatig hindi sa pamamagitan ng mga numero, ngunit sa pamamagitan ng mga titik, ang lahat ay pamilyar dito. Sa mga unang aralin ng algebra, palaging ito ay mahirap para sa maraming mga mag-aaral. Alalahanin kung gaano kahirap noong una na masanay sa pagdaragdag ng mga titik sa halip na mga numero, paglutas ng mga equation na walang sinasabi.

Marahil, ang bawat isa sa atin pagkatapos ay nagtanong sa ating sarili sa tanong na: "Bakit kailangan nating magpasok ng mga titik sa halip na mga numero at kinakailangan ba ito?" At sa paglaon lamang nakita mo kung ano ang ibinibigay ng algebra kapag naglutas ng mga problema kumpara sa aritmetika.

Ginagamit ang Algebra sa maraming eksaktong agham. Ito ay pisika, mekanika, sopromat, koryente. Batas ng Ohm wala nang higit pa sa isang equation ng algebraic: sapat na upang mapalitan ang kanilang mga numerical na halaga sa halip na mga titik upang malaman kung ano ang kasalukuyang dumadaloy sa pagkarga, o kung ano ang paglaban ng isang seksyon ng circuit.

Kaya't nakilala mo ang algebra ng mga numero, o sa elementong algebra. Ang pangunahing at halos natatanging gawain ay upang makakuha ng sagot sa tanong: "Ano ang X katumbas? Magkano? "

Sa high school, pinag-aaralan nila ang mga simula ng vector algebra. Ang algebra na ito ay panimula na naiiba sa elementong algebra. Ito ay may ibang katangian ng set ng pinag-aralan at iba pang mga patakaran ng pagkilos. Paglutas ng equation ng vector, nakakuha kami ng sagot sa isang vector na hindi isang ordinaryong numero na sumasagot sa tanong na "Magkano?"

Ang mga pormula ng vector algebra ay nasa maraming respeto na naiiba sa mga formula ng elementong algebra. Halimbawa, sa elementarya algebra at sa vector algebra mayroong isang karagdagan sa operasyon. Ngunit ginagawa ito sa ganap na magkakaibang paraan.Ang pagdaragdag ng mga numero ay hindi pareho sa pagdaragdag ng mga vectors.

Mayroong iba pang mga algebras: linear algebra, algebra ng mga istraktura, algebra ng mga singsing, algebra ng lohika, o, ano ang parehong bagay, Boolean algebra. Hindi mo marinig ang pangalan sa mga aralin sa paaralan. George Boole - ngunit alam ng lahat ang pangalan ng isa sa kanyang mga mahuhusay na anak na babae na si Ethel Voinich (1864 - 1960). Isinulat niya ang nobelang "Gadfly", na pinag-uusapan ang pakikibaka para sa mga karapatan ng mga Italian carbonarians.

Si George Bull ay ipinanganak sa Inglatera noong Nobyembre 2, 1815. Sa buong buhay niya ay nagtrabaho siya bilang isang guro ng matematika at pisika sa paaralan. Mula sa mga memoir ng kanyang mga mag-aaral ay kilala kung ano ang kahalagahan ng Bul na nakakabit sa pagbuo ng mga kakayahan ng malikhaing mag-aaral. Sa paglalahad ng bagong materyal, hinahangad niyang matiyak na ang kanyang mga mag-aaral mismo ay "natuklasan muli" ang ilang mga pormula at batas.

Sa pagsasabi sa mga mag-aaral tungkol sa mga paghihirap na hindi kinaya ng mga siyentipiko sa paghahanap para sa katotohanan, ginusto ng guro na ulitin ang isang karunungan sa Silangan: kahit na ang trono ng Persia ay hindi maaaring magdulot ng labis na kasiyahan sa isang tao bilang pinakamaliit na natuklasan sa siyentipiko. Hindi nawalan ng pag-asa si Buhl na balang araw ay makagawa ng isang tunay na pagtuklas ang kanyang mga mag-aaral.

Ang hanay ng mga pang-agham na interes ng Buhl ay napakalawak: siya ay pantay na interesado sa matematika at lohika - ang agham ng mga batas at anyo ng pag-iisip. Sa mga panahong iyon, ang lohika ay itinuturing na agham na humanities, at marami ang nakakaalam kay George Boole ay namangha sa kung paano ang eksaktong mga pamamaraan ng kognisyon na likas sa matematika at pulos naglalarawang pamamaraan ng lohika ay maaaring magkakasamang magkasama sa isang tao.

Ngunit nais ng siyentipiko na gawin ang agham ng mga batas at anyo ng pag-iisip bilang mahigpit tulad ng alinman sa mga natural na agham, sabi ng matematika at pisika. Para sa mga ito, nagsimula ang Boule na magpahiwatig ng hindi bilang bilang mga titik, tulad ng ginagawa sa ordinaryong algebra, ngunit ang mga pahayag, at ipinakita na ang mga naturang equation, na halos kapareho sa mga algebraic, ay maaaring malutas ang mga katanungan tungkol sa katotohanan at kasinungalingan ng mga pahayag na ginawa ng tao. Kaya ang Boolean algebra ay bumangon.

Ngunit hindi nagtagal bago si George Buhl, ang Aleman na matematiko at pilosopo na si Gottfried Leibniz (1646-1716) ay unang dumating sa ideya ng paglikha ng isang agham na magtatalaga ng lahat ng mga konsepto ng ordinaryong kolokyal na pagsasalita sa mga simbolo at magtatag ng ilang bagong algebra para sa pagsasama ng mga simbolo na ito.

Matapos ang paglikha ng nasabing agham, ayon kay Leibniz, ang mga siyentipiko at pilosopo ay titigil sa pagtatalo at pagsigaw sa bawat isa, alamin ang katotohanan, ngunit kukuha sila ng isang lapis at kalmadong sabihin: "Alamin natin!"

Ngayon, ang algebra ng logic ay naging isang mahalagang bahagi ng matematika. Ang isa sa mga gawain nito ay upang malutas ang lahat ng mga uri ng mga equation, ang mga bilang ng mga ratio na kung saan ay pinalitan ng mga alpabetikong. Ang bawat isa sa iyo, marahil, sa buong buhay mo naalala kung paano malutas ang mga equation ng pangalawa at pangatlong degree na may mga coefficients ng sulat. Kaya, ginamit ni Boole sa kanyang bagong algebra ang lahat ng mga pormula at panuntunan na ito.

Ano ang bago sa Boolean algebra ay ang mga elemento ng set na pinag-aralan dito ay hindi mga numero, ngunit mga pahayag. Kung, kapag nalutas ang ordinaryong mga equation ng algebra, tinutukoy kung anong bilang ang hindi kilalang X ay pantay, hinahanap ng algebra ng paaralan ang sagot sa tanong: "Magkano?"

Ang algebra ng lohika ay naghahanap ng sagot sa tanong na: "Ito ba o ang pahayag na ito na tinukoy ng titik X totoo?"

Ang kahulugan at nilalaman ng pahayag ay hindi gumaganap ng anumang papel dito. Ang bawat pahayag ay maaari lamang maging totoo o mali. Hindi ito maaaring maging kalahati ng totoo at kalahating hindi totoo. Bilang halimbawa, maaari nating isipin ang paghagis ng maraming pera sa isang barya.

Dalawang estado ng barya lamang ang isinasaalang-alang doon - ulo o buntot. Sa pamamagitan ng kasunduan ng mga partido, ang agila ay OO, at ang mga buntot ay HINDI. Walang iba pang mga intermediate point na isinasaalang-alang sa probabilidad teorya, kahit na posible. Ang isang flipped barya ay maaaring mahulog sa isang gilid, igulong ang sahig sa mga binti ng isang upuan o mesa at manatili sa isang patayo na posisyon, o kahit na nahulog sa isang malawak na agwat sa sahig. (Sa pamamagitan ng pagkakatulad sa mga de-koryenteng circuit, ang huling dalawang sitwasyon ay maaaring isaalang-alang bilang isang madepektong paggawa sa anyo ng isang nasunog na contact).Ngunit sa mga panahong iyon, ang Boolean algebra, sayang, ay hindi malawak na ginagamit.

Si Claude Shannon ay "natuklasan" muli ang Buhl algebra. Noong 1938, habang nag-aaral pa rin sa Massachusetts Institute of Technology at America, pinatunayan ng batang Claude na ang Boolean algebra ay ganap na angkop para sa pagsusuri at pagbubuo ng relay at paglipat ng mga circuit.

Sa tulong ng Boolean algebra, napakadaling gumawa ng isang de-koryenteng circuit ng isang automaton na operating sa isang relay.Para sa mga ito, lumiliko ito, kailangan mo lamang malaman kung ano ang dapat gawin ng makina, iyon ay, kailangan mong magkaroon ng isang algorithm para sa pagpapatakbo nito. Kaya ang pundasyon ay inilatag para sa teorya ng mga digital machine na nagpapatakbo sa prinsipyo ng OO o HINDI.

Ang nasabing, sa madaling sabi, ay ang kasaysayan ng Boolean algebra. Sa mga sumusunod na artikulo ay isasaalang-alang natin ang mga pangunahing batas, halimbawa ng mga contact circuit na nagpapatupad ng mga batas na ito. Isaalang-alang ang solusyon ng mga gawaing iyon na ibinigay sa simula ng artikulo.

Pagpapatuloy ng artikulo: Boolean algebra. Bahagi 2. Pangunahing mga batas at pagpapaandar

Boris Aladyshkin