Boolean algebra. Bahagi 2. Pangunahing mga batas at pagpapaandar

Pagpapatuloy ng kwento tungkol sa Boolean algebra, kumbensyon, panuntunan, operasyon. Paglipat sa mga pangunahing kaalaman ng mga circuit ng contact.

Sa unang artikulo Inilarawan si George Bull bilang tagalikha ng algebra ng lohika. Ilalarawan ng pangalawang artikulo ang mga pangunahing operasyon ng Boolean algebra, at mga pamamaraan para sa pagpapagaan ng mga expression ng Boolean. Kaya, ang Boolean algebra ay gumagamit ng mga pahayag bilang mga argumento, at hindi ang kahulugan nito, ngunit ang katotohanan o kasinungalingan ng pahayag.

Ang form para sa pagsulat ng mga expression sa Boolean algebra.

Kung ang pahayag ay totoo, pagkatapos ito ay nakasulat na tulad nito: A = 1, kung ito ay hindi totoo, kung gayon A = 0 (pagkatapos ng lahat, hindi totoo na ang patatas ay isang prutas). Para sa anumang pahayag, ang A ay alinman sa totoo (A = 1) o mali (A = 0). Maaaring walang gitna dito. Napag-usapan na natin ito.

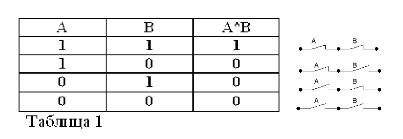
Kung ikinonekta mo ang dalawang simpleng pahayag sa unyon At, nakakakuha ka ng isang kumplikadong pahayag, na kung saan ay tinatawag na isang lohikal na produkto. Magsagawa tayo ng dalawang simpleng kasabihan: "Tatlo ay higit sa dalawa" itatalaga namin sa pamamagitan ng titik A, "Tatlong mas mababa sa lima" - sa pamamagitan ng sulat B.

Samakatuwid ang kumplikadong pahayag na "Tatlo ay higit sa dalawa At mas mababa sa lima" ay isang lohikal na (sa kasong ito, ang kabisera ng titik At, sinabi na ito ay isang "AT" lohikal na operasyon, pati na rin sa paglaon sa teksto na "O" at "HINDI.") at B. Ito ay itinalaga bilang mga sumusunod: A ^ B o A * B.

Mga lohikal na pagpaparami (operasyon "AT").

Sa elementarya algebra A * A = A2. Ngunit sa algebra ng Buhl, ang A * A = A2 = A, A * A = A mula nang ang sign multiplikasyon (*) ay nangangahulugang ... At ... sa kahulugan ng And ... At. Ang lahat ng aming karanasan ay nagpapatunay na ang A&A ay pareho sa A. nag-iisa. Ang isa ay hindi maaaring sumang-ayon dito. Ang katotohanan ng pahayag ay hindi magbabago kung paulit-ulit ito sa pamamagitan ng kadahilanan ng maraming beses.

Ang produkto ng dalawang pahayag ay itinuturing na totoo (katumbas ng 1), kung gayon, at kung ang parehong mga kadahilanan ay totoo, at hindi totoo (katumbas sa 0) kung hindi bababa sa isa sa mga salik ay hindi totoo. Sumang-ayon na ang mga patakarang ito ay hindi sumasalungat sa pangkaraniwang kahulugan, at, bilang karagdagan, ganap nilang sinunod ang mga patakaran ng elementong algebra:

1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.

Ang unang pagkakapantay-pantay ay nagbabasa ng mga sumusunod: kung pareho ang A at B ay totoo, kung gayon ang produkto A * B ay totoo. Sa Buhl algebra, ang pagpaparami ng sign (*) ay pumalit sa unyon I.

Ang mga lohikal na produkto ay maaaring magsama hindi dalawa, ngunit isang mas malaking bilang ng mga pahayag - mga kadahilanan. At sa kasong ito, ang produkto ay totoo lamang kapag sa parehong oras ang lahat ng mga pahayag-kadahilanan ay totoo.

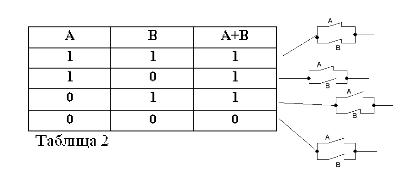
Lohikal na karagdagan (O operasyon)

Kung ang dalawang pahayag ay konektado ng isang unyon O. na nabuo ng tambalang pangungusap ay tinatawag na isang lohikal na kabuuan.

Isaalang-alang ang isang halimbawa ng isang lohikal na kabuuan. Sinasabi ang A: "Ngayon pupunta ako sa sinehan."

Pahayag B: "Ngayon pupunta ako sa disco." Nagdagdag kami ng parehong mga pahayag at nakakakuha ng: "Ngayon pupunta ako sa mga pelikula O sa isang disco."

Ang komplikadong pahayag na ito ay minarkahan tulad ng sumusunod: A + B = C o (A V B) = C.

Sa pamamagitan ng C tinukoy namin ang isang kumplikadong pahayag ng isang lohikal na kabuuan.

Sa halimbawa na isinasaalang-alang, ang unyon O ay hindi maaaring gamitin sa isang eksklusibong kahulugan. Sa katunayan, sa parehong araw maaari kang makapunta sa sinehan at sa disco. At narito ang kasabihan:

"Ang chairman ng pagsasamahan sa paghahardin ay si Petrov o Ivanov," ay hindi isang lohikal na kabuuan, dahil isang tao lamang ang magiging chairman, at ang isa ay magiging isang amateur ordinaryong hardinero.

Ang V sign para sa lohikal na kabuuan ay pinili dahil ito ang paunang titik ng salitang Latin na "vel", ibig sabihin "o", kaiba sa salitang Latin na "aut>, na nangangahulugang" at ". Ngayon dapat itong maging malinaw sa lahat kung bakit ang produktong lohikal na ay ipinahiwatig ng pag-sign ^.

Sa elementarya algebra mayroong isang panuntunan A + A = 2A. Ang panuntunang ito ay totoo, kahit na anong numero ang kinakatawan ng letrang A. Sa Boolean algebra, ang panuntunan A + A = A tumutugma dito.Ang buong karanasan sa ating buhay ay nagsasabi na ang sabihin O A o pareho ang A ay isa pa at mas mahabang paraan upang sabihin lamang A.

Tulad ng anumang pahayag na tambalan, ang kabuuan ng dalawang pahayag na A at B ay maaaring maging totoo o mali. Ang kabuuan ay itinuturing na totoo, iyon ay, katumbas ng pagkakaisa, kung hindi bababa sa isa sa mga termino ay totoo:

A + B = 1 kung O A = 1 O B = 1, na naaayon sa maginoo aritmetika:

1+0 = 0+1 = 1.

Kung ang parehong mga kabuuan ng mga pahayag ay totoo, kung gayon ang kabuuan ay itinuturing din na totoo, samakatuwid, sa Boolean algebra mayroon tayo: (1) + (1) = 1.

Ang mga bracket ay nakalagay dito upang bigyang-diin ang kondisyunal, ang kahulugan ng karagdagan, at hindi aritmetika.

Ang kabuuan ng dalawang pahayag ay itinuturing na mali at pantay sa zero kung, at kung ang parehong mga term ay hindi totoo. Mula rito:

0 + 0=0.

Kaya, ang kabuuan ng dalawang pahayag na A + B ay itinuturing na totoo kung totoo, O A, O B, O parehong magkakasamang termino. Kaya, ang salitang O ay tinukoy ng +.

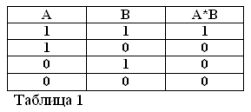
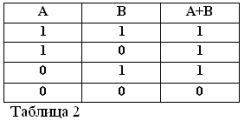
Ang pag-alala na ang mga pahayag na A at B ay maaaring maging totoo o mali at, samakatuwid, ay may isang sukatan ng katotohanan 1 o 0, ang mga resulta ng isinasaalang-alang na AT at O ​​operasyon ay maaaring ibubuod sa mga talahanayan 1 at 2.

Ang pangatlong operasyon, na malawakang ginagamit ng Buhl algebra, ay ang negation operation - HINDI. Paalala namin sa iyo na ang elementong algebra ay gumagamit ng mga operasyon ng ADD, D Magbawas, Multiply ng, Hatiin, at ilang iba pa.

Para sa bawat pahayag A, mayroong negation nito na HINDI A, na ating isasaad ng simbolo / A. Hindi ito dapat pag-aalinlangan.

Nagbibigay kami ng mga halimbawa: "Pupunta kami sa kagubatan" A, "Hindi kami pupunta sa kagubatan" / A

Kung ang pahayag A ay totoo, iyon ay, A = 1, kung gayon ang negation nito / A ay dapat na mali / A = 0. At kabaliktaran, kung ang anumang pahayag ay hindi totoo, kung gayon ang negasyon nito ay totoo. Halimbawa: "Ang kabayo ay hindi kumakain ng dayami" / A = 0, "Ang isang kabayo ay hindi kumakain ng dayami" (A = 1). Maaari itong ipahayag sa talahanayan 3.

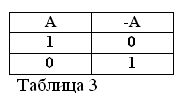
Ang pagtukoy ng kahulugan ng pagkilos ng negasyon, at ipinapalagay na sa dalawang pahayag na A at / A ay palaging isang totoo, dalawang bagong formula ng alpebra ng Boolean:

A + (/ A) = 1 at A * (/ A) = 0.

Mayroon ding iba pang mga pormula na nagpapagaan ng lohikal na pagproseso ng mga pahayag. Halimbawa, ang 1 + A = 1, dahil, ayon sa kahulugan ng pagdaragdag, sa kaso kung ang isang term ay pantay sa pagkakaisa, ang kabuuan ay palaging pantay sa pagkakaisa. Ang resulta na nakuha ay hindi nakasalalay kung A = 0 o A = 1.

Ang bawat isa sa tatlong mga lohikal na operasyon na sinuri natin (AT, O, HINDI) ay may ilang mga pag-aari na malapit sa mga patakaran ng elementong algebra. Kung ang lahat ng mga ito ay nakabalangkas, pagkatapos ay nakakakuha kami ng 25 mga patakaran ng Boolean algebra. Sapat na ang mga ito upang malutas ang halos anumang lohikal na problema. Kung wala ang mga patakarang ito, nagiging mahirap na malutas ang mga lohikal na problema dahil sa kanilang maliwanag na pagiging kumplikado. Ang sinusubukan upang mahanap ang tamang sagot nang hindi ginagamit ang mga patakaran ay nangangahulugang palitan ang mga ito ng talino sa paglikha at pangkalahatang pangangatuwiran. Ang mga patakaran na lubos na mapadali ang gawaing ito at makatipid ng oras.

Sa loob ng balangkas ng artikulo imposibleng isaalang-alang ang lahat ng 25 patakaran na ito, ngunit ang mga nais ay laging mahanap ang mga ito sa may-katuturang panitikan.

Tulad ng nabanggit na sa unang artikulo noong 1938, ang batang Amerikanong siyentipiko na si Claude Shannon sa kanyang artikulong "Simbolikong Pagsusuri ng Relay at Paglipat ng Circuits" sa kauna-unahang pagkakataon ay gumagamit ng Boolean algebra para sa mga problema ng teknolohiya ng relay. Ang pagtuklas ni Shannon ay natanto niya na ang pamamaraan ng pagdidisenyo ng mga relay machine at electronic computer ay talagang isang sangay ng matematika na lohika.

Madalas itong nangyayari. Sa loob ng maraming taon, ang siyentipiko ay nagtatrabaho sa isang problema na tila hindi kinakailangan sa kanyang mga kababayan - masaya lang. Ngunit ang mga dekada at kung minsan ay lumipas ang mga siglo, at ang isang teorya na walang nangangailangan ay hindi lamang nakakakuha ng karapatang umiral, ngunit kung wala ito karagdagang pag-unlad ay hindi maiisip.

Ano ang nakatulong kay Shannon sa pangalawang pagkakataon na "tuklasin" ang Boolean algebra? Kaso? Walang anuman.

Ang pag-ibig ng mga relay machine, na binuo sa maginoo switch at relays, nakatulong sa batang siyentipiko upang ikonekta ang isang nakalimutan na teorya sa mga gawain ng awtomatikong pagpapalitan ng telepono, kung saan siya ay nagtrabaho sa oras na iyon. Kasunod nito, ipinakilala ni Shannon ang parehong ideya ng "oo o hindi" sa mga mensahe ng discrete at inilatag ang pundasyon para sa isang buong seksyon ng cybernetics - teorya ng impormasyon.

Ang algebra ni Buhl ay angkop para sa pagsusuri at synthesis ng mga relay circuit. Ito ay sapat na upang tanggapin bilang isang totoong pahayag: "May isang senyas sa circuit", at bilang isang maling - "Walang signal sa circuit", bilang isang bagong algebra lumitaw - ang signal algebra, ang relay circuit algebra.

Ang bagong algebra ay may bisa lamang para sa pagsasaalang-alang ng relay at paglipat ng mga circuit. Pagkatapos ng lahat, sa mga nasabing pamamaraan lamang ang kondisyon na "mayroong isang senyas" at "walang signal" nasiyahan. Kung saan patuloy na nagbabago ang signal, pagkuha ng isang di-makatwirang malaking bilang ng mga intermediate na kondisyon (tulad ng isang senyas ay tinatawag na analog), ang relay algebra ay hindi naaangkop. Dapat itong laging alalahanin. Ngunit ang karamihan sa mga elektronikong computer at cybernetic machine ay gumagamit ng discrete na prinsipyo ng pagproseso ng signal, na batay sa mga elemento na "oo - hindi".

Ang pananalitang "Contact sarado" ay tinanggap ni Shannon bilang totoo (1), at "Bukas na makipag-ugnay" bilang maling (0). Ang natitirang bahagi ng "algebra", kasama ang mga operasyon AT, O, at HINDI at 25 mga panuntunan, hiniram ni Shannon mula sa Boole.

Ang relay circuit algebra ay naging mas simple kaysa sa Boolean algebra, dahil nakikipag-ugnayan lamang ito sa mga elemento ng uri ng "oo - hindi". Bilang karagdagan, ang bagong algebra ay mas visual.

Ang mga elemento sa algebra na ito ay ang mga contact, na ipakikilala namin sa pamamagitan ng mga titik A, B, C ... Ang contact ay sarado - A, ang contact ay bukas - / A (sulat na may isang gitling).

Ang notasyon, tulad ng nakikita mo, ay ganap na nakuha mula sa Boolean algebra. Ang isang bukas na contact ay isang negation ng isang closed contact. Ang parehong contact ay hindi maaaring maging sarado at bukas.

Sumasang-ayon kami na kung sa anumang circuit ng dalawang contact ay minarkahan ng parehong sulat, kung gayon nangangahulugan ito na lagi silang kumukuha ng parehong mga halaga.

Sa anumang naibigay na sandali, pareho silang bukas sa parehong oras, o pareho ay sarado. Ang pinakamadaling paraan upang isipin ang mga ito nang awtomatikong konektado nang magkasama upang pareho silang magbukas o magsara.

Kung sa ilang kadena ang isang contact ay isang negasyon ng isa pang contact, kung gayon ang kanilang mga kahulugan ay palaging kabaligtaran. Halimbawa, ang mga contact C at / C ay hindi maaaring sabay-sabay na buksan o sabay sarado. At sa diagram maaari silang mailalarawan sa mekanikal na konektado: kung ang isa sa kanila ay bubukas, pagkatapos ang iba pang magsasara.

Sinimulan namin ang aming kakilala sa relay algebra sa pamamagitan ng pagsusuri ng pinakasimpleng mga circuit na nauugnay sa mga operasyon ng AT, O, at HINDI.

Ang produkto ng dalawang contact (operasyon AT) ay ang circuit na nakuha bilang isang resulta ng kanilang serye na koneksyon: ito ay sarado (pantay sa 1) lamang kapag ang parehong mga contact ay sarado (pantay sa 1).

Ang kabuuan ng dalawang mga contact (O operasyon) ay ang circuit na nabuo kapag sila ay konektado kahanay: sarado ito (katumbas ng 1) kapag hindi bababa sa isa sa mga contact na bumubuo ng circuit ay sarado (pantay sa 1).

Ang kabaligtaran ng contact na ito (operasyon HINDI) ay isang contact na katumbas sa 0 (bukas) kung ang contact na ito ay 1 (sarado), at kabaligtaran.

Tulad ng sa Boolean algebra, kung ang mga contact ay minarkahan ng mga titik A at B, pagkatapos ay ipakikilala natin ang produkto ng dalawang contact ng A * B, ang kabuuan ng A + B, at ang pakikipag-ugnay sa tapat ng A, ni / A. Ang nasa itaas ay ipinaliwanag sa mga numero 1, 2 at 3.

Katunayan ng mga talahanayan na naaayon sa AT, O, at HINDI operasyon. ngayon walang dapat maging pagdududa.

Manatili tayo sa dalawang halimbawa: 1 * 0 = 0 at 1 + 0 = 1.

Makikita mula sa figure na ang isang permanenteng sarado na contact na konektado sa serye na may isang palaging bukas na contact ay katumbas ng isang permanenteng bukas na contact (1 * 0 = 0) Ang isang permanenteng saradong contact na konektado kahanay sa isang patuloy na bukas na contact ay katumbas ng isang permanenteng saradong contact.

Ang pagkakaroon ng pamilyar sa aritmetika ng mga contact circuit, maaari mong ilarawan ang anumang circuit ng relay na may pormula gamit ang tinanggap na mga kombensiyon. Sa mga cybernetics, ang mga naturang formula ay tinatawag na istruktura.

Kung ang pormula ng istruktura ng anumang circuit ng relay ay 1, kung gayon ang isang senyas ay maaaring dumaan dito - sarado ang circuit. Sa kabaligtaran, kung ang pormula ng istruktura ng circuit ay 0, ang signal ay hindi dumadaan dito - ang circuit ay nasira.Konklusyon: ang dalawang mga relay circuit ay katumbas sa bawat isa kapag ang kanilang mga istruktura na pormula ay pantay.

Sa pagpapatuloy ng artikulo, isasaalang-alang namin ang mga halimbawa ng mga circuit ng contact, karaniwang mga circuit ng contact at ang kanilang mga katumbas, pati na rin ang pagguhit ng mga diagram ayon sa mga pormula sa istruktura. Isaalang-alang din namin ang pangunahing mga lohika na circuit na gumaganap ng mga pag-andar ng Boolean algebra.

Pagpapatuloy ng artikulo: Boolean algebra. Bahagi 3. Mga scheme ng pakikipag-ugnay

Boris Aladyshkin

Comments

[#1 Alex]

Salamat sa iyo

Isang punto lamang, talata:

"Tulad ng sa Boolean algebra, kung ang mga contact ay minarkahan ng mga titik A at B, pagkatapos ay ipakikilala natin ang produkto ng dalawang contact ng A * B, ang kabuuan ng A + B, at ang pakikipag-ugnay sa tapat ng A, ni / A. Ang nasa itaas ay ipinaliwanag sa Mga figure 1, 2, at 3 ..."

Nasaan ang figure 3?