Mga kategorya: Itinatampok na Mga Artikulo » Praktikal na Elektronika
Bilang ng mga tanawin: 32001
Mga puna sa artikulo: 2
Mga capacitor sa mga electronic circuit
Sa mga nakaraang artikulo, pinag-usapan namin sandali ang pagpapatakbo ng mga capacitor sa AC circuit, kung paano at bakit ipinapasa ng mga capacitor ang AC sa kasalukuyan (tingnan - AC Capacitors) Sa kasong ito, ang mga capacitor ay hindi nag-init, ang kapangyarihan ay hindi inilalaan sa kanila: sa isang kalahating alon ng sinusoid, ang singil ng kapasitor, at sa iba pa, natural itong naglalabas, habang inililipat ang naka-imbak na enerhiya pabalik sa kasalukuyang mapagkukunan.
Ang pamamaraang ito ng pagpasa sa kasalukuyang nagbibigay-daan sa iyo upang tawagan ang kapasitor ng isang libreng paglaban, at sa gayon ang dahilan kung bakit ang kapasitor na konektado sa outlet ay hindi gumagawa ng pag-ikot ng counter. At ang lahat ng ito ay dahil ang kasalukuyang nasa kapasitor ay nangunguna sa eksaktong 1/4 ng oras na inilapat ang boltahe dito.
Ngunit ang phase advance na ito ay posible hindi lamang upang "linlangin" ang counter, ngunit ginagawang posible upang lumikha ng iba't ibang mga circuit, halimbawa, mga generator ng sinusoidal at hugis-parihaba na signal, oras ng pagkaantala at iba't ibang mga dalas na filter.
Sa proseso ng kuwentong ito, kakailanganin nating alalahanin kung minsan ang nasabi na, bago magsalita, upang magbubuod. Makakatulong ito na huwag bumalik sa mga naunang artikulo upang maalala ang isang simpleng pormula, o simpleng, "ano ito?"
Parallel at serye na koneksyon ng mga capacitor
Sa pamamagitan ng isang magkakatulad na koneksyon ng mga capacitor, ang kabuuang kapasidad ay simpleng aritmetika na kabuuan ng mga kapasidad. Naturally, sa pagsasama na ito, ang kabuuang kapasidad ay magiging mas malaki kaysa sa kapasidad ng pinakamalaking kapasitor. Ctotal = C1 + C2 + C3 + ... + Cn.
Sa kaso ng isang serye na koneksyon, ang kabuuang kapasidad ay mas mababa kaysa sa pinakamaliit.
1 / Ctotal = 1 / C1 + 1 / C2 + 1 / C3 + ... + 1 / Cn.
Kapag ang dalawang magkaparehong capacitor ay konektado sa serye, ang kabuuang kapasidad ay magiging katumbas sa kalahati ng kapasidad ng isa: halimbawa, kapag kumokonekta sa dalawang capacitor na 1 µF bawat isa, ang kabuuang kapasidad ay magiging 0.5 µF.
Kakayahan Xc
Dito, ang lahat, tulad ng kung ang pagkonekta sa mga resistor, ay eksaktong eksaktong kabaligtaran: ang isang koneksyon sa serye ay binabawasan ang kabuuang kapasidad, habang ang isang paralel ay pinatataas ito. Ang sitwasyong ito ay hindi dapat kalimutan kung kumokonekta ang mga capacitor, dahil ang isang pagtaas sa capacitance ay humantong sa isang pagbawas sa kapasidad Xc
Xc = 1/2 * π * f * C.
Mula sa punto ng matematika, ito ay lubos na natural, dahil ang kapasidad C ay nasa denominator ng maliit na bahagi. Sa pamamagitan ng paraan, ang dalas f ay nasa parehong lugar, kaya ang isang pagtaas sa dalas ay humahantong din sa isang pagbawas sa kapasidad Xc. Ang pisikal na kahulugan nito ay sa pamamagitan ng parehong kapasitor ito ay mas mahusay, mas hindi nasasaktan, na ang mataas na dalas ay pumasa. Tatalakayin ito ng kaunti makalipas, pagdating sa mga low-pass at high-pass filter.
Kung kukuha tayo ng isang kapasitor na may kapasidad na 1 μF, kung gayon para sa dalas ng 60 Hz nito Xc ay magiging 2653 Ohms, at para sa isang dalas ng 400 Hz ang parehong kapasitor ay may Xc na 398 Ohms lamang. Ang mga nagnanais ay maaaring suriin ang mga resulta sa pamamagitan ng pormula, pagpapalit ng π = 3.14, ang dalas sa hertz, at ang kapasidad sa mga pamasahe. Pagkatapos ang resulta ay nasa ohms. Ang lahat ay dapat sumunod sa SI system!
Ngunit ang mga capacitor ay ginagamit hindi lamang bilang free-damping damping resistances o sa mga rectifier filter. Kung wala ang kanilang pakikilahok, ang mga circuit para sa mga mababa at mataas na dalas ng mga generator, iba't ibang mga pag-convert ng alon, nagkakaiba at pagsasama ng mga circuit, mga amplifier at iba pang mga scheme.
Susunod, isasaalang-alang ang iba't ibang mga de-koryenteng senyas na dapat gawin ng mga capacitor. Una sa lahat, ito ay mga pana-panahong signal na angkop para sa pagmamasid sa oscilloscope.
Panahon at dalas ng mga oscillation
Ang isang pana-panahong pag-oscillation ay tinatawag na pana-panahong, na, nang walang pagtigil, inuulit ang parehong form, halimbawa, isang sinusoidal na pag-oscillation. Ang tagal ng buong swing na ito ay tiyak na tinatawag na panahon T, at sinusukat sa mga segundo, milliseconds, microseconds.Ang mga makabagong elektroniko ay nakikipag-usap din sa mga nanosecond (isang bilyong segundo).
Ang bilang ng mga panahon bawat segundo ay tinatawag na dalas (gaano kadalas) ng mga oscillations f, at ipinahayag sa hertz. Ang 1Hz ay ang dalas kung saan ang isang pag-oscillation, isang buong panahon, ay isinasagawa sa 1 segundo. Ang ratio ng panahon at dalas ay ipinahayag ng simpleng pormula T = 1 / f.
Alinsunod dito, alam ang panahon ng pag-oscillation, napaka-simple upang makalkula ang dalas f = 1 / T.
Ito ay kung paano ang pagkalkula ay kinakalkula kapag sinusukat sa isang oscilloscope: ang bilang ng mga selula sa isang panahon ay kinakalkula, pinarami ng tagal ng isang cell, at ang panahon ay nakuha, halimbawa, sa microseconds. At upang malaman ang dalas, ginamit lamang nila ang huling formula.
Ordinaryo elektronikong osilkopyo Pinapayagan kang obserbahan lamang ang mga pana-panahong signal na maaaring ma-synchronize sa dalas ng pagwalis upang makakuha ng isang imahe na angkop para sa pananaliksik. Kung magpadala ka ng isang senyas sa isang programa ng musika sa pag-input ng oscilloscope, hindi mo mapigilan ang imahe para sa anupaman. Upang obserbahan ang gayong mga senyas, ginagamit ang storage oscilloscope.
Kung ang isang panahon ay sinusukat sa milliseconds, ang dalas ay nakuha sa kilohertz, para sa isang panahon na sinusukat sa microseconds, ang dalas ay ipinahayag sa megahertz. Ito ay kung hindi mo sinusunod ang mga kinakailangan ng system ng SI: panahon sa ilang segundo, dalas sa hertz.
Hindi pang-sinusoidal na panginginig
Tulad ng nabanggit kanina, ang isang sine wave ay ang pinaka-karaniwang at angkop para sa pag-aaral at praktikal na paggamit ng pana-panahong curve. Sa mga kondisyong pang-industriya, nakuha ito gamit ang mga electric generator, halimbawa, sa mga hydroelectric power halaman. Sa mga elektronikong aparato, ginagamit ang mga panginginig ng boses ng pinaka-iba't ibang mga hugis.
Karaniwan, ang mga ito ay tatlong mga form: sinusoidal, hugis-parihaba at tatsulok, tulad ng ipinapakita sa Figure 1. Ang parehong kasalukuyang at boltahe ay maaaring magkaroon ng tulad ng isang hugis, samakatuwid, ang figure ay nagpapakita lamang ng axis ng oras, ang ordinate axis ay naiwan nang walang pangalan.
Ang ganitong mga oscillation ay nabuo ng mga espesyal na elektronikong circuit. Ang mga hugis-parihaba at tatsulok na senyas ay madalas na tinatawag na pulsed. Gayunpaman, maraming mga electronic circuit na nagsasagawa ng conversion ng signal: halimbawa, isang parihaba, isang tatsulok ay maaaring gawin mula sa isang sinusoid.
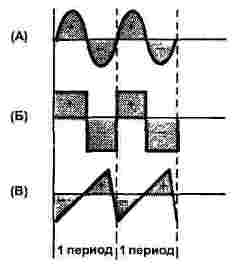
Larawan 1
Para sa lahat ng tatlong mga senyas, ang figure ay nagpapakita ng dalawang panahon, ang lahat ng mga signal ay may parehong dalas.
Spectrum ng mga di-sinusoidal signal
Ang anumang signal ng kuryente ay maaaring kinakatawan bilang isang pagsukat ng amplitude sa ilang oras sa oras. Ang dalas ng mga halimbawang ito ay tinatawag na sampling frequency, at hindi bababa sa dalawang beses na mas mataas kaysa sa itaas na dalas ng sinusukat na signal. Pagkatapos mula sa mga halimbawang ito, maaari mong ibalik ang orihinal na signal. Ginagamit ang pamamaraang ito, halimbawa, sa digital na pag-record ng tunog. Ang pamamaraang ito ay tinatawag ding pagtatasa ng oras.
Ipinapalagay ng isa pang pamamaraan na ang anumang signal, kahit isang hugis-parihaba, ay maaaring kinakatawan bilang algebraic na kabuuan ng mga sinusoids na may iba't ibang mga frequency at phase. Ang pamamaraang ito ay tinatawag na frequency analysis. Ngunit, ang sinabi "na may iba't ibang mga frequency" ay hindi ganap na totoo: ang nasasakupang mga sinusoids ay tinatawag na magkatugma at ang kanilang mga dalas ay sumusunod sa ilang mga batas.
Ang isang sine wave na ang dalas ay katumbas ng dalas ng isang parisukat na alon ay tinatawag na pangunahing o unang maharmonya. Kahit na ang mga harmonika ay nakuha sa pamamagitan ng pagpaparami ng pangunahing dalas sa pamamagitan ng isang numero, at kakaibang mga pagkakaisa, ayon sa pagkakabanggit, sa pamamagitan ng kakatwa.
Kaya, kung ang unang maharmonya ay may dalas ng 1000 Hz, kung gayon ang pangalawa ay 2000 Hz, ang pang-apat ay 4000 Hz, atbp. Ang mga kakatwang magkakatugma ay magkakaroon ng dalas ng 3000Hz, 5000Hz. Bukod dito, ang bawat maharmonya ay mas maliit sa amplitude kaysa sa pangunahing: mas mataas ang maharmonya, mas maliit ang malawak.
Sa musika, ang mga harmonika ay tinatawag na mga pang-abay. Sila ang bumubuo ng timbre ng tunog, ginagawang posible upang makilala ang biyolin mula sa piano, at ang gitara mula sa saxophone. Hindi nila pinapayagan na malito ang tinig ng lalaki at babae o makilala ang Petrov kay Ivanov. At ang sinusoid mismo ay hindi na maaaring mabulok o magtipon mula sa anumang mga signal.
Ipinapakita ng Figure 2 ang pagtatayo ng isang hugis-parihaba na pulso.
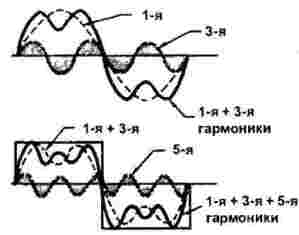
Larawan 2
Ang una at pangatlong harmonika ay ipinapakita sa itaas na bahagi ng pigura. Madali itong makita na sa isang panahon ng unang maharmonya tatlong mga panahon ng ikatlong pass. Sa kasong ito, ang malawak ng ikatlong harmonic ay isang ikatlo sa una. Ang kabuuan ng una at pangatlong harmonika ay ipinapakita din dito.
Sa ibaba, kasama ang kabuuan ng 1 at 3 na magkatugma, ipinapakita ang isa pang 5 na magkatugma: para sa isang panahon ng isang parihabang signal na pinamamahalaan nitong gawin nang eksaktong limang yugto. Sa kasong ito, ang amplitude nito ay mas maliit, mas tumpak, eksaktong 1/5 ng pangunahing (una) ng isa. Ngunit hindi dapat isipin ng isang tao na ang lahat ay nagtatapos sa ikalimang maharmonya: hindi lamang ito maipakita sa pigura, sa katunayan marami pa.
Ang pagbuo ng mga sawtooth at tatsulok na signal, na ipinakita sa Figure 3, ay medyo mas kumplikado.Kung sa nakaraang kaso tanging kakaibang mga pagkakaisa ang naganap, kung gayon ang mga pagkakaarmonya ay naglalaro.
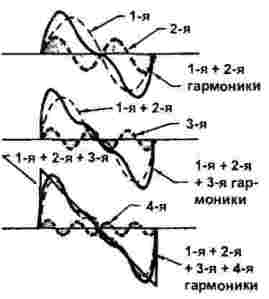
Larawan 3
Sa gayon, maipahayag namin ang katotohanan na sa tulong ng maraming mga harmonika ang isang senyas ng anumang hugis ay synthesized, at ang bilang at uri ng mga harmonika ay nakasalalay sa pagbabago ng alon, tulad ng ipinapakita sa Mga figure 2 at 3.
Kapag nag-aayos at mag-set up ng elektronikong kagamitan, ginagamit ang isang oscilloscope upang pag-aralan ang mga signal ng elektrikal. Pinapayagan ka nitong isaalang-alang ang anyo ng mga pana-panahong signal, ang kanilang kalakasan, sukatin ang panahon ng pag-uulit. Ngunit ang mga harmonika na ipinakita sa Mga figure 2 at 3 ay hindi makikita.
Kahit na kumonekta ka, halimbawa, isang electric gitara sa isang oscilloscope, hilahin ang isang string, lumilitaw ang isang sinusoid sa screen, ito rin ang unang maharmonya. Sa kasong ito, walang pag-uusap tungkol sa anumang mga pag-atake. Ang parehong sinusoid ay magreresulta kung pumutok ka sa pipe o plauta sa harap ng mikropono.
Paano makakuha ng mga hugis-parihaba na impulses
Matapos makilala ang mga signal ng elektrikal, kailangan nating alalahanin ang mga capacitor kung saan nagsimula ang artikulo. Una sa lahat, dapat mong makilala ang isa sa mga klasikal na circuit ng elektroniko - multivibrator, (Larawan 4) ito ay siya na bumubuo ng mga hugis-parihaba na pulses. Napaka-klasik ng circuit na nagsisimula itong gumana kaagad nang hindi nangangailangan ng anumang mga setting o pagsasaayos.
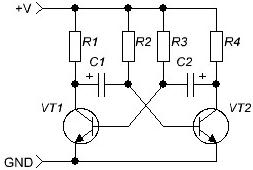
Larawan 4
Ang multivibrator ay isang dalawang yugto ng amplifier, na sakop ng positibong puna. Kung ang mga kolektor ng pag-load ng kolektor R1 = R4, ang mga resistors ng base R2 = R3 at ang capacitor C1 = C2 ay pantay, ang multivibrator ay tinatawag na simetriko at bumubuo ng mga square pulses ng alon ng uri ng meander - ang tagal ng pulso ay katumbas ng tagal ng pag-pause.
Ang cycle ng tungkulin ng naturang mga pulso (ang ratio ng panahon sa tagal ng pulso) ay katumbas ng dalawa. Sa mga wikang Ingles na mga scheme, ang lahat ay eksaktong kabaligtaran: tinawag nila itong duty cycle. Ito ay kinakalkula bilang ang ratio ng tagal ng pulso sa panahon ng tagumpay nito at ipinahayag bilang isang porsyento. Kaya, para sa meander, 50% ang duty cycle.
Tama ba ang computer?
Ang pangalang multivibrator ay iminungkahi ng Dutch physicist van der Pol, dahil ang spectrum ng isang hugis-parihaba na signal ay naglalaman ng maraming mga pagkakaisa. Maaari mong i-verify ito kung maaari kang maglagay ng isang tatanggap ng radio na nagpapatakbo sa daluyan ng saklaw ng alon malapit sa isang multivibrator na gumagana kahit sa isang dalas ng audio: ang mga howl ay magmumula sa speaker. Ipinapahiwatig nito na bilang karagdagan sa dalas ng tunog, ang multivibrator ay nagpapalabas din ng mga mataas na dalas na mga oscillation.
Upang matukoy ang dalas ng henerasyon, maaaring magamit ng isa ang formula f = 700 / (C1 * R2).
Sa form na ito ng formula, ang kapasidad ng capacitor sa microfarads (μF), ang paglaban sa kilo-ohms (KΩ), ang resulta sa hertz (Hz). Kaya, ang dalas ay tinutukoy ng pare-pareho ng oras ng circuit C1 * R2; ang mga naglo-load ng kolektor ay hindi nakakaapekto sa dalas. Kung kukuha tayo ng C1 = 0.02 μF, R2 = 39 KΩ, pagkatapos ay makakakuha tayo ng f = 700 / (0.02 * 39) = 897.4 Hz.
Multivibrator sa edad ng mga computer at mga microcontroller Ayon sa pamamaraan na ito, halos hindi kailanman ginagamit, kahit na maaaring angkop ito para sa iba't ibang mga eksperimento. Una sa lahat, gamit ang mga computer. Ganito ang hitsura ng circuit ng multivibrator sa programa ng Multisim. Ang koneksyon ng oscilloscope ay ipinapakita rin dito.
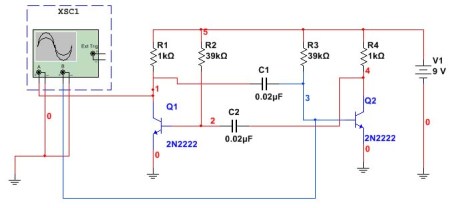
Larawan 5
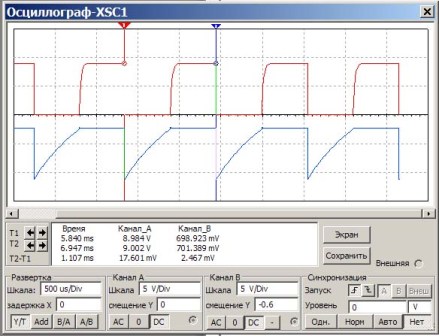
Sa circuit na ito, ang mga capacitor at resistors ay naka-install tulad ng sa nakaraang halimbawa. Ang gawain ay suriin ang pagkalkula ayon sa pormula kung ang parehong dalas ay makuha. Upang gawin ito, sukatin ang panahon ng mga pulses, at pagkatapos ay muling pagkalkula ang mga ito sa dalas. Ang resulta ng Multisim oscilloscope ay ipinapakita sa Figure 6.
Larawan 6
Ang ilang mga paglilinaw sa Larawan 6.
Sa screen ng oscilloscope, ipinapakita ng pulang pulso ang mga pulses sa kolektor ng transistor, at ang asul sa mga base. Sa ibaba ng screen sa isang malaking puting window, ipinapakita ng mga numero ang mga resulta ng pagsukat. Kami ay interesado sa haligi na "Oras". Ang oras ay sinusukat ng mga tagapagpahiwatig T1 at T2 (pula at asul na tatsulok sa itaas ng screen).
Kaya, ang panahon ng pag-uulit ng pulso T2-T1 = 1.107ms ay ipinakita nang tumpak. Ito ay nananatiling lamang upang makalkula ang dalas f = 1 / T = 1 / 1.107 * 1000 = 903Hz.
Ang resulta ay halos kapareho ng pagkalkula ayon sa pormula, na binibigyan ng kaunti mas mataas.
Ang mga capacitor ay maaaring gamitin hindi lamang nang hiwalay: sa kumbinasyon ng mga resistors, pinapayagan ka nitong simpleng lumikha ng iba't ibang mga filter o lumikha ng mga phase-shift circuit. Ngunit tatalakayin ito sa susunod na artikulo.
Pagpapatuloy ng artikulo: Mga capacitor sa mga electronic circuit. Bahagi 2
Boris Aladyshkin
Tingnan din sa electro-tl.tomathouse.com
: