Ano ang koneksyon sa pagitan ng mga seksyon ng wire at populasyon ng kuneho?

Noong 1202, inilathala ng dalubhasang matematiko na si Leonardo Fibonacci ang kanyang gawain sa ilalim ng pamagat na "Aklat ng Abacus" ("Book of Calculations"), kung saan inilarawan din niya ang bilang ng serye na imortalize ng kanyang pangalan. Sa isa sa mga kabanata, sinubukan ng Fibonacci na ipakita sa matematika kung paano tataas ang bilang ng mga kuneho. Isinasaalang-alang niya ang mga sumusunod na hypotheses bilang mga kondisyon:

1) ang unang dalawang buwan ng isang pares ng mga rabbits ay hindi nagbibigay ng mga supling;

2) simula sa ikatlong buwan, ang isang pares ng mga kuneho ay nagbibigay ng isa pang pares ng mga kuneho.

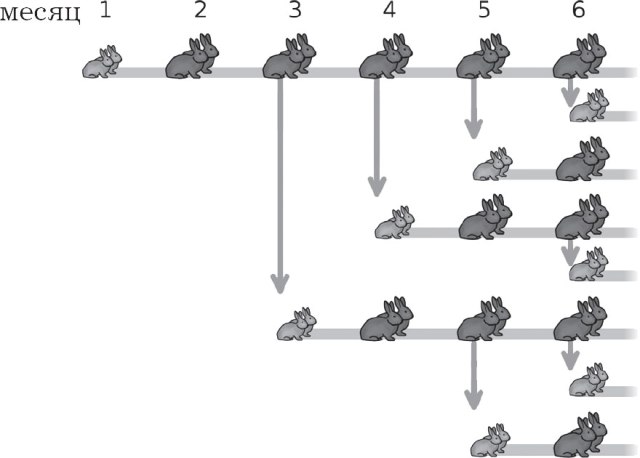
Bilang isang resulta ng pagbuo ng isang pattern ng paglago ng populasyon ng kuneho, nakuha namin ang mga sumusunod na serye ng mga numero, na pinapansin ang pagtaas ng bilang ng mga rabbits bawat buwan:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 …

1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5; 3 + 5 = 8…

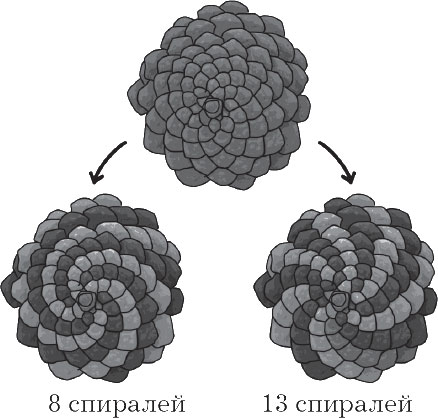
Kung maingat mong tiningnan ang paga, makikita mo na ang ibabaw nito ay binubuo ng mga kaliskis na baluktot sa isang spiral alinsunod sa pagkakasunud-sunod ng Fibonacci. Habang sa isang pinya o sa isang bulaklak ng isang mirasol, nakikita sila sa hubad na mata.

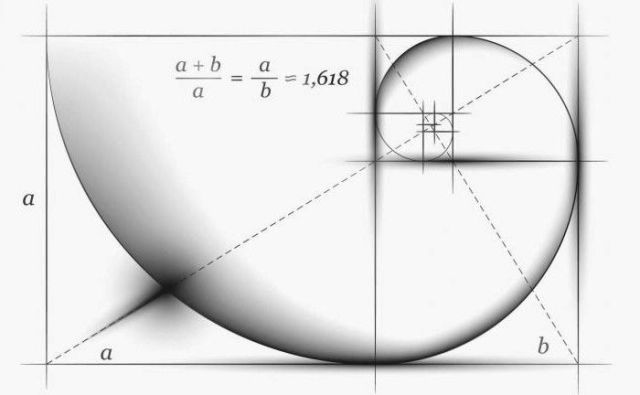
Dahil ang oras ng Antiquity ng Golden Ratio, ang bilang = 1.618. Itinuring ng mga sinaunang Greeks ang halaga ng perpektong proporsyon. Ang gintong ratio ay ang ratio ng bawat kasunod na numero sa serye ng Fibonacci sa nakaraang isa:

144/89=89/55=55/34=34/21=21/13=13/8=8/5=5/3=1,618...

Ginamit ito ng mga sinaunang Greeks sa arkitektura. Ang harapan ng Parthenon sa Athens ay may katulad na mga proporsyon na may isang rektanggulo na itinayo sa prinsipyo ng ginintuang ratio.

Kaya ano ang kagandahan ng pagkakasunud-sunod ng mga seksyon ng kawad, na-rate ang mga alon ng mga electric at cutoff na alon ng mga circuit breaker? Bumuo ng isang serye ng mga numero na may mga sumusunod na halaga: 1,5; 2.5; 4; 6; 10; 16; 25; 40; 63...

Na-rate na mga alon ng mga electromagnetic na nagsisimula:

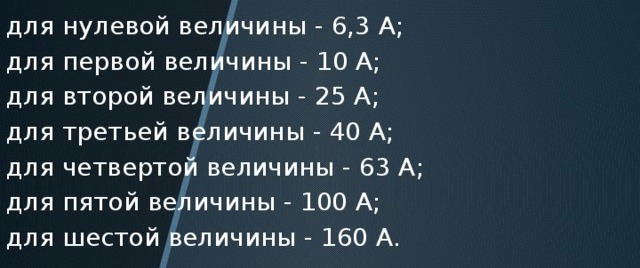
Kaya kung hatiin mo ang 2.5 / 1.5; 4 / 2.5; 6.3 / 4; 10 / 6.3; 16/10; 25/16; 40/25; 63/40pagkatapos makuha namin ang tungkol sa 1.6. Alin ang tumutugma sa panuntunan ng ginintuang ratio. At sumasalamin sa kagandahan at henyo ng kalikasan kahit na sa aming mga boring na sistema ng engineering.

Ano sa palagay mo? Ito ba ay isang aksidente?

Batay sa aklat na "Isang mahusay na nobelang tungkol sa matematika. Kasaysayan ng mundo sa pamamagitan ng prisma ng matematika" ni Michael Lone. Salamat sa rekomendasyon mula sa Vladimir Kisel.

Alexey Bushnyaga